【数据结构笔记（一）基本概念与时间复杂度计算

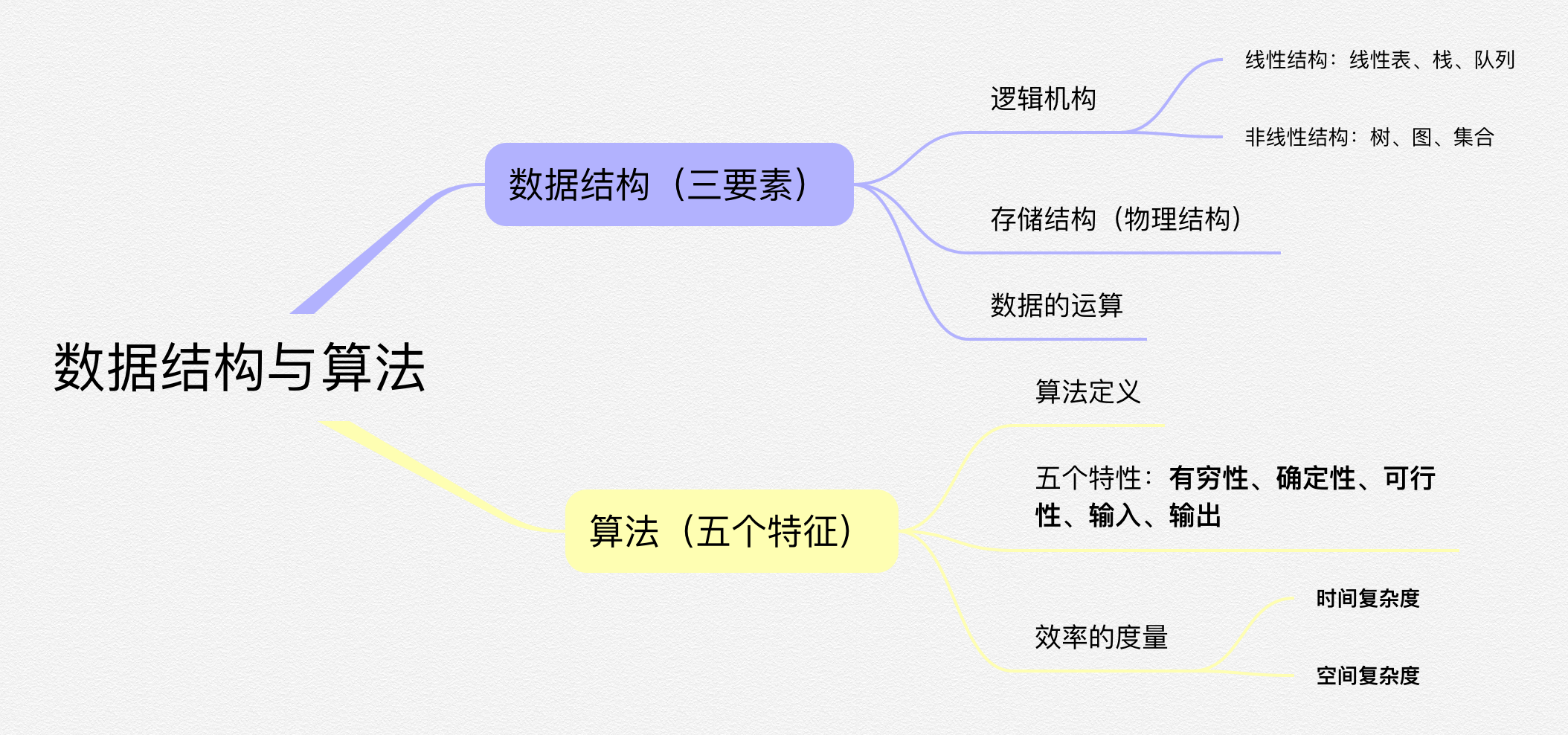
一、 相关概念

• 数据结构（Data Structure）是相互之间存在一种或多种特定关系的数据元素的集合。
• 算法（Algorithm）是对特定问题求解步骤的一种描述，它是指令的有限序列，其中每一条指令表示一个或多个操作。
• 时间复杂度（Time complexity）是一个定性描述该算法的运行时间的函数，是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述。
  • 最坏时间复杂度是指在最坏情况下，算法的时间复杂度。
  • 平均时间复杂度是指所有可能输入实例在等概率出现情况下，算法的时间复杂度。
  • 最好时间复杂度是指在最好情况下，算法的时间复杂度。
• 空间复杂度（Space Complexity）定性地描述该算法或程序运行所需要的存储空间大小，是相应计算问题的输入值的长度的函数，它表示一个算法完全执行所需要的存储空间大小。空间复杂度常用大O符号表述。

二、 时间复杂度计算

2.1 两条规则

• 加法规则

  T(n) = T1(n) + T2(n) = O(f(n)) + O(g(n)) = O(max(f(n), g(n)))

• 乘法规则

  T(n) = T1(n) * T2(n) = O(f(n)) * O(g(n)) = O(f(n) * g(n))

T(n)：算法中所有语句的频度之和，是算法问题规模 n 的函数。

f(n)（或g(n)）：算法中基本运算的频度。其中，基本运算为最深层循环内的语句。

• 常见的（渐近）时间复杂度：

O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(n³) < O(2ⁿ) < O(n!) < O(nⁿ)

2.2 计算方法

• 循环主体中的变量参与循环条件判断：

  1. 设基本运算执行 k 次
  2. 将变量结果代入循环终止条件公式
  3. 反解出 k

• 循环主体中的变量与循环条件无关：

  • 递归程序：

    1. 将问题规模 设为 n 或其他方便计算的值（如 2^k)
    2. 将问题规模代入递推公式
    3. 将递推公式由 T(n) 格式转化为 T(1) 格式。其中，T(n) 为递推公式递归条件下的公式，T(1) 为基线条件下的临界值
    4. 解出T(n)

  • 非递归程序：

    可由公式 T(n) = Σ…Σ基本运算 计算得出。其中 Σ 上下值为循环变量的临界值和初始值，Σ 个数为嵌套循环的个数

三、典型例题

1. 有以下算法，其时间复杂度为：（ ）

   y = 0;
   while((y + 1) * (y + 1) <= n) 
   					y = y + 1;
   

2. 【2012年计算机联考真题】求正数 n (n ≥ 0) 阶乘的算法如下，其时间复杂度是（ ）

   int fact(int n) {
   	if(n <= 1) return 1;
   	return n * fact(n-1);
   }
   

3. 一个算法所需时间由下述递归方程表示，试求出该算法的时间复杂度的级别（或阶）。

   \(T(n)=\left\{\begin{array}{ll} 1 & \text { 右 } n=1 \\ 2 T(n / 2)+n & \text { 若 } n>1 \end{array}\right.\) 式中，n 是问题的规模，为简单起见，设 n 是2的整数次幂。

4. 程序段

   for(i = n - 1; i > 1; i--)
   	for(j = 1; j < i; j++)
   		if(A[j] > A[j+1])
   			swap(A[j], A[j+1]);
   

   其中 n 为正整数，则最后一行语句频度在最坏情况下是（ ）

5. 【2013年计算机联考真题】已知两个长度分别为 m 和 n 的升序链表，若将它们合并为一个长度为 m+n 的降序链表，则最坏情况下的时间复杂度是（ ）

答案：1: O(n^1/2); 2: O(n); 3: O(nlogn); 4: O(n²); 5: O(max(m,n))

四、思考题

求解斐波那契数列：\(F(n)=\left\{\begin{array}{ll}1 & n=0,1 \\ F(n-1)+F(n-2) & n>1\end{array}\right.\) 有两种常用的算法：递归算法和非递归算法。试分别分析两种算法的时间复杂度。